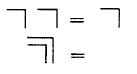An Esoteric Guide to Spencer Brown’s Laws of Form #4
« Previous Page | 1 2 3 4 | View All | Next Page »
(New readers will want to start with the first installment.)
We ended the last installment having come to realize something of the esoteric significance of the taijitu, or yin-yang, form, in something of an extended tangent. We return now to the text.
GSB himself seemed to understand the importance of the Laws of Form, even if there were some of these more subtle specifics which were not apparent to him (or at least which he did not explicitly recognize). Having reached this point (literally we are still on page 1 of LoF), the vast majority of the rest of the work in LoF is seen to be secondary. Yet there are many valuable indications which deserve connection to esoteric principles, and the point of this exploration is to show that such connections are not arbitrary. So, to return to the actual content of LoF now, after this long but foundational detour, we can note that he says:
LoF p. 5
- Let any token [of the mark] be intended as an instruction to cross the boundary of the first distinction.
That is, every mark is an invitation to cross it; every distinction is a call to make that distinction, not to simply point it out, but also to DO it, to MAKE the distinction. In other words, the whole thing is ACTIVE, not passive, it is not descriptive but PRESCRIPTIVE. Of course, the esoteric significance of this should be obvious, because precisely what distinguishes esoteric work from, say, philosophy or other disciplines, is that it is, at its roots, injunctive. That mathematics is the discipline most closely allied to esoteric work in this respect only serves to strengthen the indication that mathematics is the most spiritual of academic disciplines.
Now, if you don’t know, GSB uses LoF to show how, starting from one single form, he can build an entire logical calculus, including (but not limited to) the Boolean Algebra. In fact, the way he came upon the LoF was precisely through asking himself the question “what is the basic arithmetic upon which the Boolean Algebra is based?” (Esalen conference, session two).
He uses the token of the form, the upside-down and backwards “L” as an operator to do this work. The whole of the logical calculus in LoF is built out of the way that this form works with itself, and he notes that the two “primitive equations” upon which everything else is based take the form:
LoF p.11
He calls the first primitive equation number, and the second (where a form is inside itself, which equals the unmarked state) order. Why is this important? Because we can note that these two principles, upon which everything that is to follow in LoF is based, is nothing other than the embodiment, in form, of the principle of the N and N+1 orders discussed as the key to the whole thing in the first place.
To state it another way, these two primitive equations work because they embody exactly what would be required of them if they were to work (to take a GSB type of phrasing). More directly, they embody the principle of the creation of the cross and the crossing of the cross. Together, these two equations express the principles required to yield all the complexity necessary for any ontology: this means they have, together, a horizontal and vertical direction, or a breadth and depth, a distinguishing and a unifying nature. The first equation is horizontal: it serves to open up all the later logical space in LoF. The second equation is vertical: it serves to unify across levels, or to create more levels. You can see that this is just what is implied in the levels N and N+1: the level N is what it is by virtue of its containing everything else that is at level N, while the level N+1 is precisely the activity of the unification of everything in level N. N is the content, N+1 is the activity by which anything in N gets to be in N in the first place, vs. at any other level (say, N-1). The reason for calling these levels N and N+1, vs. actually counting them from some starting point should be obvious: they are recursive with each other; there can never be some absolute destination “N” that could serve to begin the counting. We can only ever count from where we actually begin.
« Previous Page | 1 2 3 4 | View All | Next Page »