The following four questions (one per post) were posed in a recent class. My edited responses follow.

1. So I understand that any shape in nature can be converted to a mathematical formula, right? Then you take that formula and plug in the variable related to that shape and feed the answer into the variable spot in the next equation, continuing that as many times as one wants (with potential infinite number of times).   Here is where I get stuck.  Does each answer produce a smaller version of the original shape or does the answer produce the snowflake-like shape of the whole, complex, product?

We do not know how to find mathematical functions for every shape in nature; indeed this is still an area of active research.  Usually we can model (i.e. approximate) natural shapes with mathematical functions, but nature is a little more slippery and variable than the stark purity of mathematics proper, so we don’t get exact results.  This isn’t usually a problem, however, because the whole point is that we can occasionally find mathematical functions that provide something of the… essence of the form.

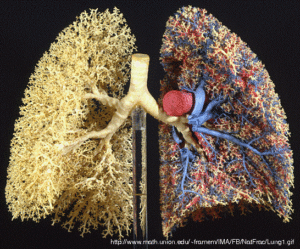
For example your lungs are fractal in nature, branching and branching and branching… but they don’t do it in only one way.  Rather, they have different ‘stages’ of branching, each with a different ‘fractal dimension’, depending on how many previous branches lie before it (I can explain what a fractal dimension is if you wish in another post).  (Read a single page about this from the Cellular and Molecular Life Sciences journal – slightly technical but you can probably get the basic idea through a different lens, which is always useful: http://www.springerlink.com/content/q103206u70402617/)

But to answer the question directly re: “each answer…”,  most fractals both occur and are described by the taking of a single set of relations (it may be a shape), and repeating that relation/shape on different scales, with rotations, translations (moving without rotating), etc.  In other words, you start with a thing and then put it through some sort of process, then take the new whole that results and do the same process to it again, and so forth.  What is interesting is that a pattern emerges out of the process… and the process is primary, NOT THE THING.  In fact, you can take ANY shape, and subject it to a specific process over and over, and you will get the SAME fractal form, regardless of the original shape.  So each iteration (“each answer”) is a further unfolding of the process, a more ‘detailed’ rendering of the pattern inherent in the unfolding of the process.

So it’s not just a question of “smaller versions” or of reproductions of the “whole”; the pattern that defines the particular fractal is really the expression of an infinite process (usually based on some pretty simple and limited rules, like “rotate 36 degrees counter-clockwise and scale by a factor of 1/2”), which can be “reversed” (rotate 36 degrees clockwise and scale by a factor of 2) – so size has nothing to do with it, and you can start anywhere in the process with whatever you have, because the thing isn’t ‘the thing’ if you know what I mean: ‘the thing’ is the process.  This is very good for nature because nature can take whatever is there and do some pretty simple things and get some very complicated results.  It doesn’t have to start with a ‘grand plan’ that requires everything to be exact and fit in just the right way in order for it to ‘work’, but can just take whatever is there and MESS AROUND.  This isn’t the whole story but I’m just trying to relate this to fractals specifically.