Feedback and levels of description, or: What MPEG2 compression can teach you about cybernetics and epistemology
A fellow student pointed out recently to me that compression algorithms are an excellent way to see feedback at work, and used the example of mpeg2 video compression. Here we have a system that utilizes multiple levels of abstraction and feedback in order to efficiently compress video data.
I will give you a picture or two and quote some relevant explanations on the process as a basis for the following discussion.
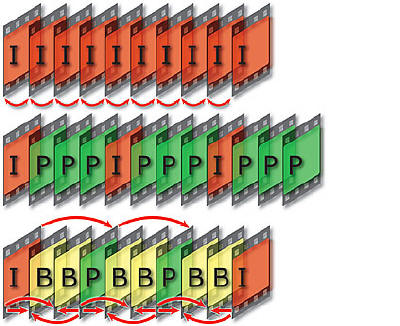
“The result of the MPEG-2 encoding process is a video stream. The basic unit of the stream is a “Group of Pictures” (GOP), made up of three picture types: I, B, and P. I-pictures (intra) are compressed using intra-frame techniques only, meaning that the information stored is complete enough to decode the frame without reference to any adjacent frames. For B (bi-directional) and P (predictive) pictures, however, only “difference information” (frame-to-frame changes) is stored, which generates much less data. These pictures can only be reconstructed by referring to the I-pictures around them, which is why the different picture types are grouped into GOPs.”
also:
“MPEG 2 provides for up to three types of frames called the I, P and B frames. The intra-frame, or ‘I’ frame, serves as a reference for predicting subsequent frames. ‘I’ frames, which occur on an average of one out of every ten to fifteen frames, only contains information presented within itself. ‘P’ Frames are predicted from information presented in the nearest preceding ‘I’ or ‘P’ frame. The bi-directional ‘B’ frames are coded using prediction data from the nearest preceding ‘I’ or ‘P’ frame AND the nearest following ‘I’ or ‘P’ frame.”
So you have completely self-contained frames, appropriately called I-frames. Then you have predictive-frames which contain information about DIFFERENCES ONLY, and which only have inputs from PAST I or P frames. But then you have bidirectional frames, which are constructed out of BOTH past and future frames (either I or P), and which also only encode differences.
This works because this type of compression operates on two levels simultaneously, the level of the FRAME CONTENT and the level of DIFFERENCES in frame content. The language of differences is a completely different language than that of the content, and constitutes (I think) a higher order of language from the type of language that can appropriately describe the content.
I’m only making this post because the content of the previous paragraph is generalizable to any system. Any system has a content-level which in some way encodes, describes, and utilizes a particular type of information (in this case, things like hue, lightness, and saturation). If the system never needed to interact with other systems (or itself in regards to this content), this would be enough. But as soon as any communication of or reflection on this information is needed, it becomes terribly inefficient to only keep to content-level languages. So in communicating or transferring that information from one epistemological system to another (a system for which the information can be of significance, i.e. produce a change), it is much more efficient to utilize a higher-order language whose primary function is to describe the content in a new way.
So this second-order language describes the description, or is information about the information. What can this second-order language contain? Essentially it contains information about DIFFERENCES in the content-level, which are not contained in the content-level itself. So I can’t describe the differences of hue, lightness, and saturation from one video frame to the next by using the language of hue, lightness, and saturation. The answer to the question: “What is the difference between a lightness value of 10 and 90?” is not itself a unit of lightness, it is a DESCRIPTION of lightness; you can’t use the answer directly and unmodified as information in the content-level system. You can’t tell your monitor to show a lightness value of “a difference of 80” DIRECTLY–you have to DECODE the difference back into the content-level language through a specific process.
What gets REALLY interesting, however, is when this kind of decoding has built in to it processes which modify the content-level data not just on the basis of the second-order language of differences (as in mpeg2 compression), but on the basis of a THIRD-order language of the difference of differences. This is like taking a description of the differences and feeding that information back into the system in a way that modifies the original information. So you have something like:
1) content-level (language of ‘raw’ data)
2) process-level (language of differences in ‘raw’ data)
3) meta-process level (language of differences of differences)
How far can this go? I have no idea; theoretically one can have an infinite number of levels, but practically I don’t think this is the case, and it has to do with the fact that there is a certain sort of separation between levels that has so far been assumed that is simply not the case. In other words, these different levels are complexly intertwined, and not capable of being separated. Each level is responsible for producing changes in other levels in various ways. The process-level, by encoding differences in the content-level, can produce changes in the content-level through appropriate decoding procedures. The same relation holds between the meta-process-level and the process-level. This also means that the meta-process level can drastically change things at the content-level. But additionally the content-level, by virtue of the type of information it contains, helps restrict the possible differences that can occur, and thus the possible ways of distinguishing differences in the process-level (it doesn’t make sense for a process-level language to encode differences about mood, temperature, or conductivity if the content-level doesn’t contain such information in the first place). So each level is like a bidirectional-frame in our video compression example, in which changes come both from ‘above’ and ‘below’.
What should be pointed out, however, is that there are SECONDARY effects which become possible with the utilization of any higher-order language. Any higher order language IS higher order because it can apply to multiple differing types and systems of data. A language of differences can be more or less strongly ‘coupled’ to a particular type of content. The closer the coupling the less easily the language can be used for descriptions of different types of data systems. The weaker the coupling, the more widely applicable the higher-order language can be to different data systems, but only at the cost of some potential loss of fidelity through the filtering out of SOME differences in favor of others.
Now here is where it gets even more interesting. The selective filtering of differences is another way of saying that each higher-order system embodies a particular epistemology. Languages about data, about differences in data, and about the differences of differences are all specific embodiments of epistemological frames. EVERY system has an epistemological frame: squirrels, lakes, crystals, and of course humans. The epistemological frame is the meta-context which admits or denies differences of a given class (temperature, color, quantity, mood, awareness…) and includes specific relations between various classes. But the epistemological frame is embedded within, arises from, and also determines the data available to the system — there is no ultimate ability to distinguish between frames and data – they each mutually produce each other.
What I distinguish distinguishes what I can distinguish. Differences differentiate my differentiating.
Epistemology determines the data available to a system for distinctions. The data available to a system determines the possible epistemologies that can make distinctions about the data (yielding capta. What is given determines what can be taken; what is taken then determines what can be given (the Latin root of data is ‘to give’, and of capta is ‘to take’).
There is no escape: we live in and create a world of paradox, which is probably enough for now.